On the Generalisation of Koopman Representations for Chaotic System Control

University of Groningen

Abstract

This paper investigates the generalisability of Koopman-based representations for chaotic dynamical systems, focusing on their transferability across prediction and control tasks. Using the Lorenz system as a testbed, we propose a three-stage methodology: learning Koopman embeddings through autoencoding, pre-training a transformer on next-state prediction, and fine-tuning for safety-critical control. Our results show that Koopman embeddings outperform both standard and physics-informed PCA baselines, achieving accurate and data-efficient performance. Notably, fixing the pre-trained transformer weights during fine-tuning leads to no performance degradation, indicating that the learned representations capture reusable dynamical structure rather than task-specific patterns. These findings support the use of Koopman embeddings as a foundation for multi-task learning in physics-informed machine learning.

Architecture Overview

Stage 1: Koopman Autoencoder Training
We train a Koopman-based autoencoder to encode raw 3D states into Koopman space (32D). This is done by teaching the model through system evolution.

Stage 2: Transformer Pre-training (Task A)
A decoder transformer model is trained on encoded states to perform next-state prediction.

Stage 3: Safety Function Fine-tuning (Task B)
The transformer is then frozen, where a multi-layer perceptron (MLP) safety head takes the last hidden layer from the transformer after processing a sequence and the current 3D state, to produce a safety value. This safety value represents the minimum control required to maintain the current trajectory within a predefined region Q, which encompasses the right butterfly wing of the Lorenz system.

Gallery

Results

Below in the table, we can see our results, where our Koopman frozen model performed best across MSE, MAE and R² metrics. This performance remains consistent whether the transformer backbone is frozen or not. The Error Accumulation charts reveal that Koopman frozen also produces fewer concentrated errors compared to the PCA baseline, which, despite low MSE scores, shows considerable dark spots indicating high sensitivity at unstable regions of the Lorenz system.

The previous animations demonstrate safety value predictions from our frozen Koopman-transformer model against ground truth values computed via a recursive algorithm. To illustrate the practical utility of these predictions, we implement a simple controller that applies interventions when trajectories approach or exit region Q, using predicted safety values to determine when and how much control is needed.

Model MSE (×10⁻⁴) MAE (×10⁻²) R²
Koopman Frozen 3.08 ± 6.55 1.16 ± 0.53 0.991 ± 0.089
Koopman Unfrozen 5.59 ± 17.14 1.20 ± 0.59 0.989 ± 0.089
PCA Physics-Informed 5.28 ± 8.83 1.48 ± 0.65 0.989 ± 0.090
PCA 16.80 ± 17.93 2.83 ± 0.98 0.983 ± 0.091

Safety function prediction performance across models mean (μ) ± standard deviations (σ). All metrics were computed on 252 test trajectories within the safety region.

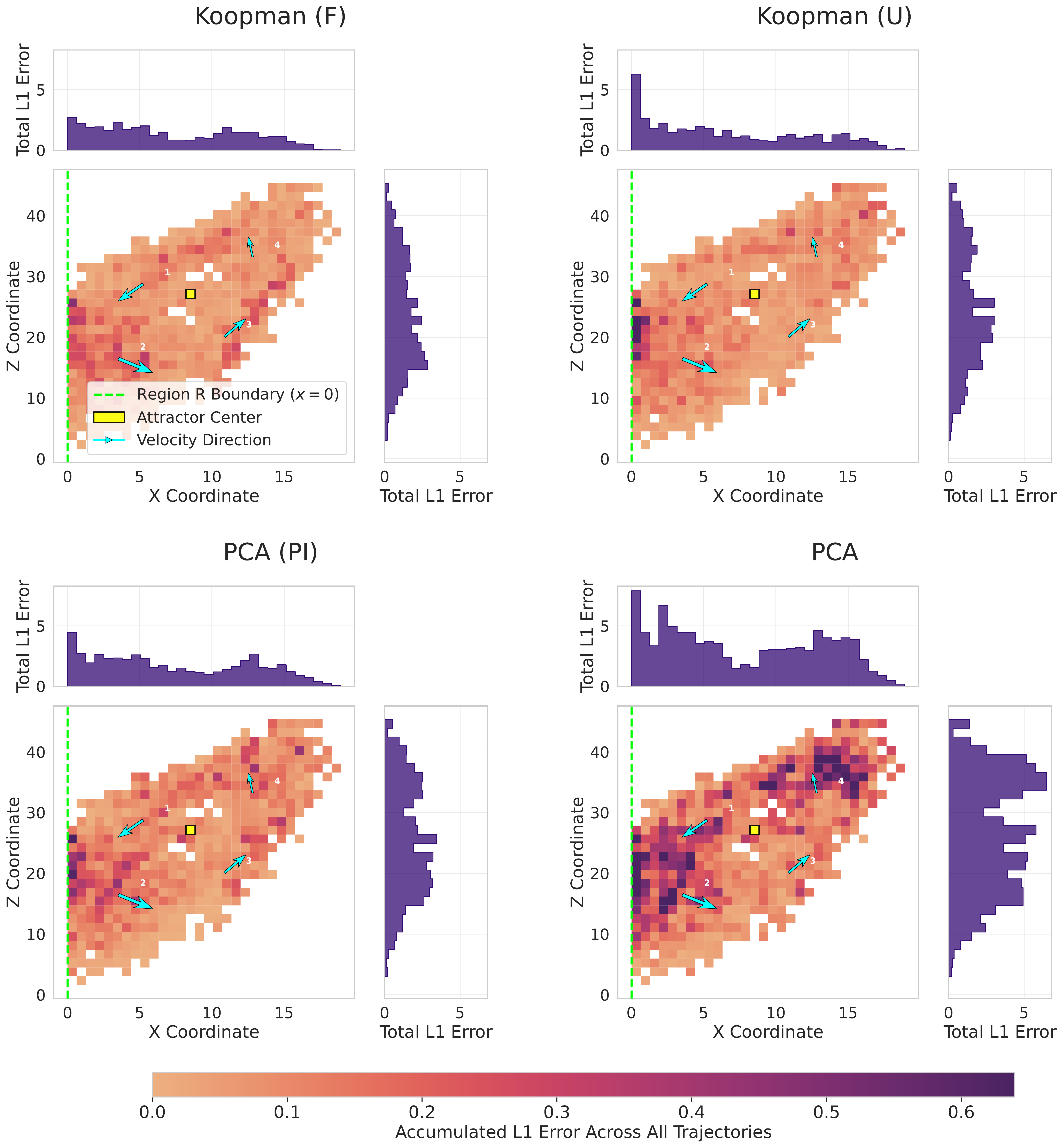
L1 Error Analysis

Comparative accumulated L1 error across the test dataset. L1 error is defined as L₁ = |y_true - y_pred|. The figure displays the X–Z projection for four models. Light regions indicate low error; darker regions represent higher error concentrations. Contextual markers denote the boundary of the training region Q (x=0), corresponding to the Lorenz attractor's equilibrium point. Vector lines show mean velocity and direction in each quadrant.